Neural Networks on the Arduino Part 1: Matrices, vectors and neural networks.

Recently I'd looked at using Python for playing with Neural Networks, with an eye to doing something hardware-ish using the Raspberry Pi. I had not realised however how "heavy" the Raspberry Pi was compared with another small computer I was already familiar with, the Arduino. (Sometimes the Arduino is called microcontroller, but it is in fact a computer.)

So I looked for examples of neural networks on the Arduino, and the only one google came up with was: A Neural Network for Arduino at the Hobbizine. I soon found that all the "neural network on an Arduino" articles I looked at pointed back to the same code. And though the code seemed to work, it was not easy to understand. It was not really organized how a neural network would be organized.

So I thought I'd make my own code for neural networks on an Arduino, it would also force me to understand the nitty gritty details.

And in the end, when you've made your neural network it will be up to you what...

1. light inputs
2. light outputs
3. motors
4. servos
5. solenoids
6. switches
7. relays
8. varistors
9. transistors
10. robots
11. robot arms
12. robot legs
13. touch sensors
14. pressure sensors
15. meteorological sensors
16. ...

...you want to use this program with! The Arduino has all inputs and outputs for a ton of fun and usefulness.

This article is not about how neural networks work, though there is a bit of that, but about how to implement them on an Arduino using matrix mathematics.

For a great step by step introduction to neural networks....

Matrix mathematics comes into it because a simple back propagation neural network consists of...

• a vector of inputs
• a vector of outputs
• a vector of hidden nodes
• a two matrices.

arranged like this:

(To give you a concrete example, the IN vector could be the pixels of a photo of a face, and the OUT vector could be the forename and surname of a person. Not on the little ol' Arduino though, not enough memory.)

So...

• The In Vector contains the question.
• The Out vector contains the answer.
• The IToHMat matrix contains the weights from the input vector to the hidden layer. 
• The Hidden vector contains the activation values, one per neuron, created by multiplying the In vector with the IToHMat, and a bit of processing.
• The HToOMat matrix contains the weights applied to the hidden values to obtain the Out vector, and a bit of processing.

An even more practical example, imagine a question which is a vector of 6 numbers and an answer which is a vector of 2 numbers, what would the neural network look like?

The first thing you have to do is work out the size of all the three vectors and the two matrices.

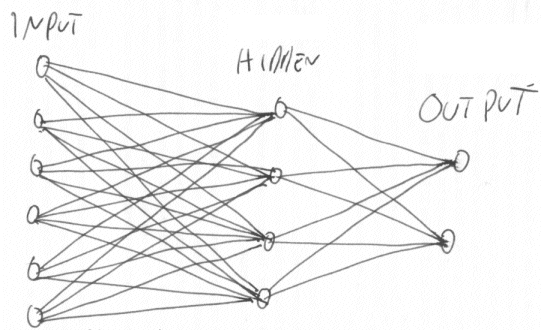
Well I've heard it said, it has been hinted that, maybe suggested, that the size of the hidden nodes vector should be, could be, may be, between the number of input and outputs. So if we have 6 inputs and 2 outputs then 4 hidden nodes would be a good guess. Here's a drawing of the neural network:

Now the connections between the input and hidden and hidden and output are most easily represented as matrices...

So in our example we know the size of all the matrices and all the vectors. The number of rows is the number of inputs and the number of columns is the number of outputs of each block of connections.

I used a mnemonic when I started studying matrix maths, RC = Roman Catholic = you have to follow the rules. The rules are:

1. Always write the size as (number of Rows) x (number of Columns), RxC.
2. When multiplying two matrices R1xC1 and R2xC2 then C1 and R2 must be equal.
3. When multiplying two matrices R1xC1 and R2xC2 then the resulting matrix is of size R1xC2

This is all illustrated better graphically:

What all this means is that once we have decided on the number  of inputs, the number of outputs and the number of hidden nodes the sizes of the two intermediate matrices are also decided for us. In Arduino C we can simply use defines like this:

#define NUM_INPUTS 6
#define NUM_HIDDEN_NODES 4
#define NUM_OUTPUTS 2

And then use those constants to create the 2 matrices as well as the 3 vectors.

I've skipped one bit in the forward action of the neural network. That is the connection between the h'1... and h1 values. The h'1... values are calculated from the h1... values using the sigmoid function, as shown below:

As an aside the sigmoid function...

...is used because

1. Whatever the input x is (from -infinity to +infinity) the output y is always between 0 and 1. This means that numbers in the network don't get extremely positively large or negatively large. As you can see above by the time x is +10, y practically is 1.0
2. It has an easy to calculate derivative, which is used in training the network by back propagation

But that is an aside, see...

...for a more detailed explanation

The sigmoid is also used for o1' to o1 etc.

And here is the function which would query a neural network on the Arduino:


// Given the inputs and the weights in the matrices calculate the outputs
void QueryTheNeuralNetwork (mtx_type* InVector, mtx_type* OutVector)
{
    // Use inputs and first matrix to get hidden node values...
    Matrix.Multiply((mtx_type*)InVector,
                    (mtx_type*)gInputToHiddenMatrix,
                    1, // rows in InputVector (a vector, so 1)
                    NUM_INPUTS, // columns in InputVector
                    NUM_HIDDEN_NODES, // columns in InputToHiddenMatrix
                    (mtx_type*)gHiddenOutputs); // This is the output of Multiply

    // Now we have values in the gHiddenOutputs
    // i.e. we have the summed weights*inputs in the hidden nodes

    // Transform hidden node values using sigmoid...
    for (int hn = 0 ; hn < NUM_HIDDEN_NODES ; hn++) {
        double OldHiddenNodeValue = gHiddenOutputs[hn] ;
        double NewHiddenNodeValue =  Sigmoid (OldHiddenNodeValue) ;
        gHiddenOutputs[hn] = NewHiddenNodeValue ;
    }

    // Do (sigmoided hidden node values) x (second matrix) to get outputs
    Matrix.Multiply((mtx_type*)gHiddenOutputs,
                    (mtx_type*)gHiddenToOutputMatrix,
                    1, // rows in HiddenVector (a row vector, so 1)
                    NUM_HIDDEN_NODES, // columns in gHiddenOutputs
                    NUM_OUTPUTS, // columns in InputToHiddenMatrix
                    (mtx_type*)OutVector); // This is the output of this function

    // Transform output node values using sigmoid...
    for (int o = 0 ; o < NUM_OUTPUTS ; o++) {
        const double OldOutputValue = OutVector[o] ;
        const double NewOutputValue = Sigmoid (OldOutputValue) ;
        OutVector[o] = NewOutputValue ;
    }

    // "answer" is now inside OutputVector!
    // and the current hidden node values are in gHiddenNodes
}

Note that there are two matrices and three vectors, just as in the diagram at the beginning of this article.

The sigmoid function in Arduino code can be written like this:

 // Implement y = Sigmoid(x)
double Sigmoid (const double x)
{
    double y = 1.0/(1.0 + exp(-x)) ;
    return y ;
}
So far so good. But how do we adjust the weights (change the matrices) during training of the neural network?  How do we do the back propagation bit? And what on earth are hidden errors?

We'll get there, here's Part 2.